Lasso回帰

Lasso Regression

Feature Selection task

動機

• Efficiency
• Interpretability(Sparsity)
  • which feature is relevant for prediction

手法1: 全部のせ

• 特徴が全くないものから始める
• 次に各特徴でRSSを比較して、その中で一番できの良い物を選ぶ
• 次に２つの特徴を選択して、その中でRSSが一番低いものを選ぶ
• これを続けると、RSSがconvergeしなくなる。そこでやめる(特徴数D)
• そこで、validationやCross validationを使って、各モデルを評価する
  • validationとCross validationを分ける
• でもこれは計算量が多すぎる(2^D+1)

手法2: Greedy Algorithms(Forward Stepsize)

• 特徴が全くないものから始める
• 全特徴から一つ選択し、一番エラーの低い特徴を咥える（ここまで一緒）
• また全特徴から１つ選択し、一番エラーの低い特徴を加える
• これを繰り返す
  • O(D²) -> At most D Steps
• この特徴は、エラーが絶対増えない。また、トレーニングエラーが手法1とおなじになる　

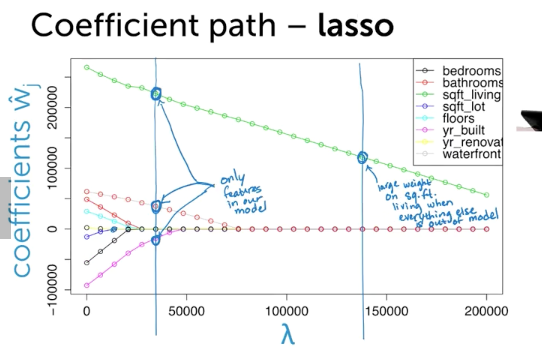
手法3: Regularize(Lasso)

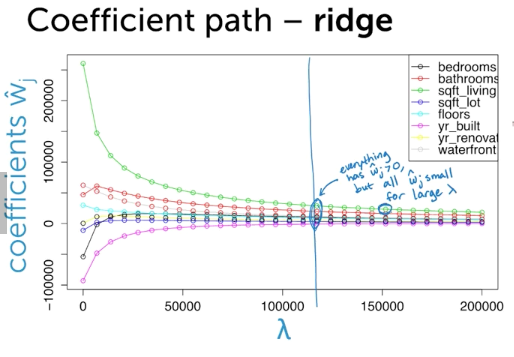
• (復習) Total Cost = measure of fit (RSS) + lambda * measure of magnitude of coefficeints(||w||^2　< - L2 norm)
  • これをL1 normにする
    • lambda still governs solution
    • lambda: tuning parameter = balance of fit and sparsity
    • lambda = 0: w_hat_lasso = w_hat_least square(unregularized solution
    • lambda = inf: w_hat_lasso = 0
    • 0 < lambda < inf: 0 <= norm(w_hat_lasso) <= norm(w_hat_least_square)
  • 小さな0以外のwが望ましい
• 全部の特徴のせモデルから初めて、いらないwを0にする手法
  • Ridge Coefficientsを閾値にかけるのは、類似した特徴がある場合に無意味。例えば# of bathroomと# of showerそれぞれのcoefficientsが低くとも、２つには相関性があるので、実質的にはそれが合算されたものであるべきであり、それは閾値を超える可能性があるから
  • Lassoを使えば、弱い特徴を0にできる（Sparsity!）

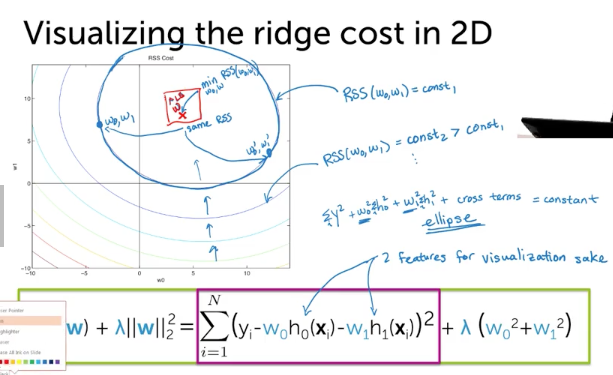
Ridge Cost in 2D

• RSS

• L2Norm

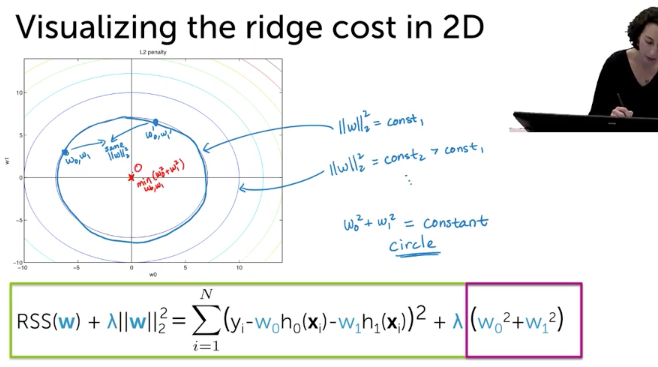
• Combined

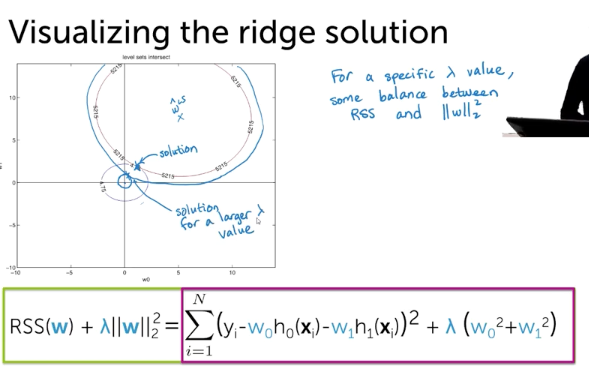
Lasso Cost in 2D

• RSS will be the same
• L1 Norm

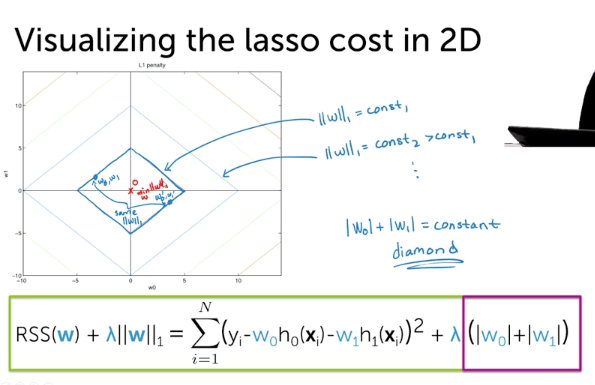
• Combined
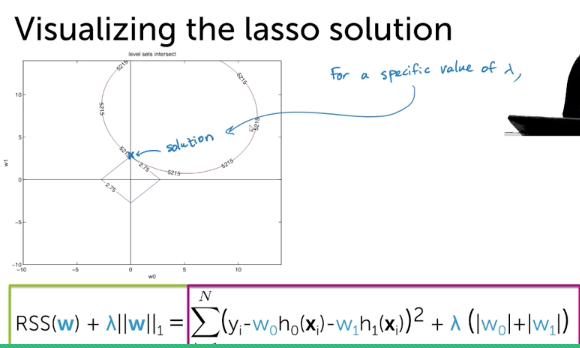
  • RSSエラーとL1Normだと、角だとSparse Solutionになる
  • hihger dimensionだと、もっとpointierなグラフになるので、角にあたりやすい

optimizing the lasso objective

• issue: derivative of |w|?
  • Critical value of derivative? -> does not exist!!
  • so do subgradients or coordinate descent
  • So no closed-form solution

Coordinate descent (Aside1)

• Converges for lasso object
• Often hard to find min for all coordinates, but easy for each coordkinate ( by fixiing others)
• NO Step Size
• How Do we pick next coordinate ?
  • random

Normalizing feature (Aside2)

• take a column data (feature) -> Scale it
• Dont forget to apply same sacle(Zj) to test data

Optimizing least squares objective one coordinate at a time (with normalized features)

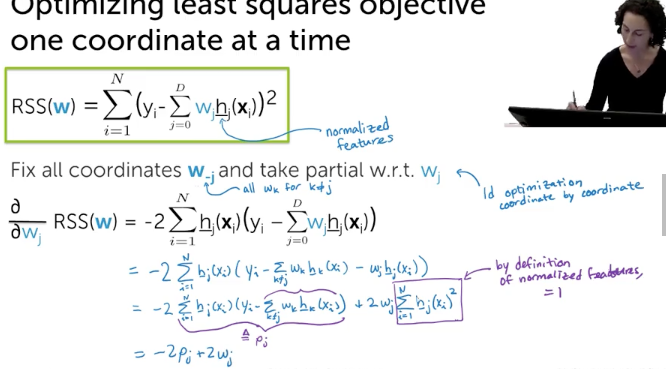
Coordinate Descent

• using soft threasholding

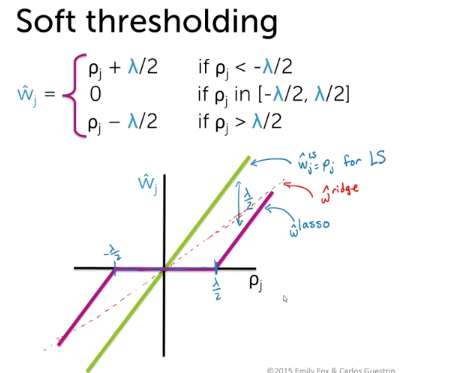
Assessing Convergence

• Max step size

How to choose lambda

• same

  • big data:divide up into traininset, validation set, test set
    • fit w_lambda, select lambda by testing performance of w_lambda, assess generalization error of best w_lambda
  • small data: k-fold cross validation

• FOr lasso, you may choose smaller lambda than optimal choice for feature selection

Practical issue

• Lasso shrinks coefficients relative to LS solution
  • more bias, less variance
    • To lessen bias... run lasso to select feature, then run ls regression with only selected features

Question

• why to sparse
• Why you want to include both correlated feature